Ключевые математические операции делятся на четыре категории – сложение (+), вычитание (-), умножение (×) и деление (÷).

Кроме вышеперечисленных существуют также: равно (=), не равно (≠), больше (>) и меньше (<), больше или равно (⩾), меньше или равно (⩽).

Все виды математических операций можно разделить на две группы:

1. Операции действия;
2. Операции отношения.

К операциям действия относятся:

• сложение
• вычитание
• умножение
• деление

К операциям отношения:

• равно
• больше или меньше
• больше или равно
• меньше или равно
• не равно

Операции отношения.

В понятие “операции отношения” входит всё, что можно соотнести друг с другом. Любые отношения, будь то размер, состояние, положение и даже взаимоотношения между людьми. Например, дружба – это пример отношения одного человека к другому. Из более простых примеров – полуторалитровая бутылка воды больше, чем литровая.

Грубо говоря, весь наш мир состоит из разных компонентов, которые так или иначе, как-то относятся друг другу.

Вернёмся к математическим значением. Если число девять больше числа четыре, мы говорим, что “девятка больше по отношению к четвёрке”. А пишем как 9 > 4 (читается как: девять больше, чем четыре). Острый угол знака > всегда направляется в сторону меньшего значения (числа). В данном случае четвёрка меньше девятки, следовательно, “клювик” символа направлен в сторону четвёрки.

Точно также читается знак < (меньше). Например число 13 меньше, чем число 17. Записать это можно таким образом:

13 < 17

Знаки операций отношений применяются во всевозможных уравнениях, формулах.

Знак = (равенства) применяется, когда две величины равны относительно друг друга.

Например, “четыре равно четырём”. Математически это можно записать так: 4 = 4. Подразумевается, что две эти четвёрки между собой равны. Возвращаясь к более сложным уравнениям, мы можем встретить и вот такие варианты:

10 + a + b = 3 + 7 + b + a

Возьмём пример из жизни: одна крупная дыня весит 6 кг, а две поменьше весят каждая по 3 кг. Следовательно, между одной большой дыней и двумя маленькими

можно поставить знак = (равенства). Читается это так: “одна дыня весом в 6 кг равна весу двух дынь по 3 кг каждая”.

А уравнение для этого примера будет выглядеть так:

6 кг = 3 кг + 3 кг

Когда две величины не равны друг другу, используется другой знак: ≠ (неравенства). Например, 10 ≠ 6. Это значит, что десятка не равна шестёрке. Другие примеры: студент не равен школьнику, корова не равна курице, рыба – это не мясо.

студент ≠ школьник

 корова ≠ курица

 рыба ≠ мясо

 На самом деле, наш мир полон математических примеров. Стоит только присмотреться, и вы найдете их вокруг себя: в классе, в своей комнате, на улице, где угодно.

Операция сложения.

Сложение в математике выглядит как знак + (“плюс”) и используется, когда складывают числа. Эти числа называются слагаемые, а результат их сложения называется суммой.

Рассмотрим операцию сложения на простом примере:

Что будет, если между цифрами 4 и 1 поставить знак + (“плюс”)?

4 + 1 = 5

В данном случае, 4 и 1 – это слагаемые. Их сумма равна 5.

Операция вычитания.

Для этой операции в математике используется знак – (минус). Он необходим, когда из одного числа нужно вычесть другое число. Исходное число, из которого нужно вычесть, называется уменьшаемое. Число, которое необходимо вычесть, называется вычитаемое. И результат этой операции называется разность.

Разберём эту операцию на примере:

7 – 4 = 3

Соответственно, 7 – это уменьшаемое, 4 – вычитается из 7, а значит, это вычитаемое. А 3 – это разность.

 Операция умножения.

 Для умножения тоже существует специальный знак ×. Его используют, когда нужно умножить числа. В отличие от сложения, умножение даёт увеличение результата в разы.

Пример: нужно умножить 5 × 2. Результатом умножения будет увеличение пятёрки в два раза, то есть 10.

Увеличивающееся число в математике называют множимое. Оно множится на определённое количество раз. Множитель – это число, которое указывает, во сколько раз увеличилось множимое. Результат умножения – произведение.

Пример:

3 × 5 = 15

В данном случае, 3 – мы определяем как множимое, 4 – как множитель. А произведение этих чисел – 15.

Чаще в школе называют первый множитель и второй множитель.

То есть в примере 3 × 5 = 15, 3 – первый множитель и 5 – второй множитель, а 15 – произведение.

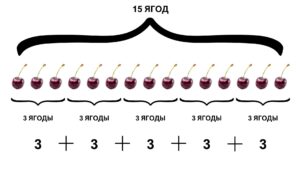
Проще говоря, умножение – это повторение (сумма) одного и того же числа (множимого) определённое количество раз. В нашем случае, это число 3. Мы повторяем его 5 раз подряд. Рассмотрим на примере ягод:

3 + 3 + 3 + 3 + 3 = 15

Мы можем взять из корзины 3 ягоды 1 раз.

3 ягоды × 1 = 3 ягоды

Попробуем сделать тоже самое дважды:

3 ягоды × 2 = 6 ягод

Итого мы возьмём за два раза 6 ягод.

А теперь возьмём ягоды из корзины ноль раз:

3 × 0 = 0

Мы ноль раз взяли из корзины ягоды, проще говоря, ни разу. Если умножить любое число на ноль, мы получим ноль.

Операция деления.

Делением пользуются, когда нужно разделить числа. Для него есть специальный знак ÷ или : (деление).

6 : 3 = 2

 В примере выше первое число 6 называется делимое. Второе число 3 – делитель. Результат операции называется частное.

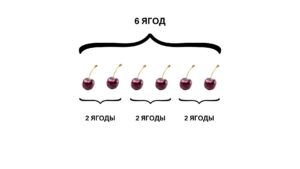
У нас есть 6 ягод. Мы делим их на 3 одинаковые части. В каждой части получится по 2 ягоды. Мы можем провести обратную операцию – умножения. 2 ягоды умножим на 3 и получим 6. В числе 6 помещается только 3 раза по 2. Поэтому, если мы разделим 6 на 3, получим 2.